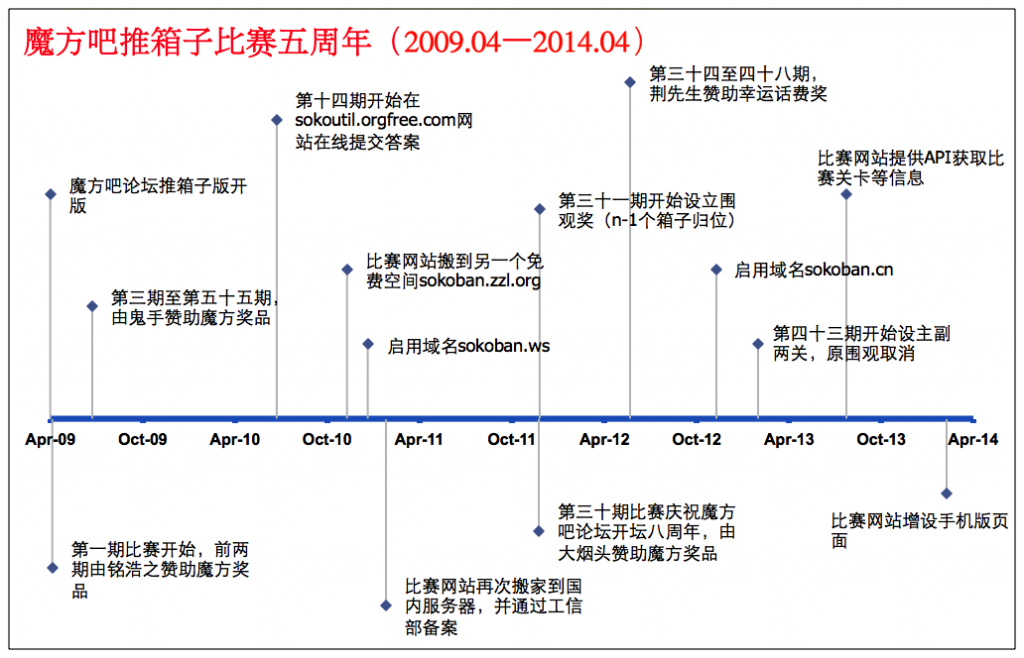
作者:楊超
本文地址:http://sokoban.ws/blog/?p=430
一
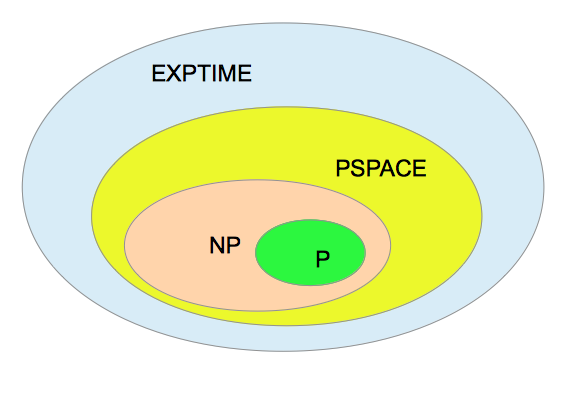
推箱子的其中一個很重要的魅力來源于推箱子求解問題在計算復雜性理論里是一個 PSPACE 完全問題。在這里不對什么是 PSPACE 完全問題作出解釋,但是推箱子的一部分美妙之處可以認為正是來源于它的計算復雜度達到了 PSPACE 完全問題的級別。具體表現就是可以設計出很多不同模式的關卡,而且我們目前所涉及到的模式只是一小部分,還有很廣闊的空間等待我們去探索。另外一個表現就是存在一系列具有指數長度答案(相對與關卡的大小)的關卡,這一類關卡就是推箱子關卡眾多模式里面非常有趣的一類,也是本文要討論的對象。
二
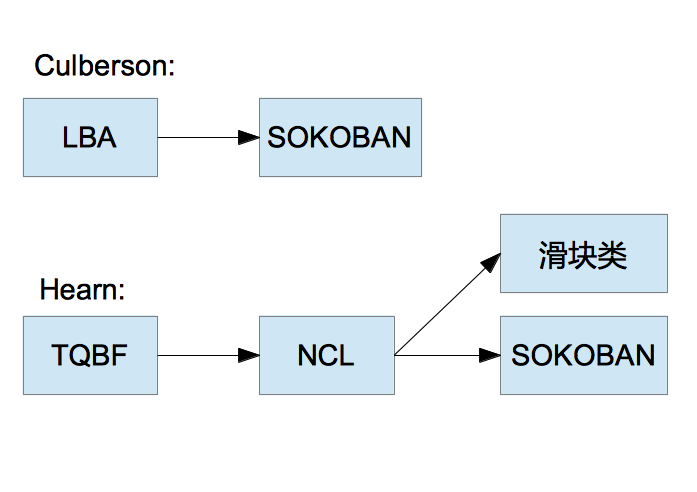
2009年6月8日,我曾在魔方吧論壇發貼子介紹了一類指數長度答案的關卡。無獨有偶,約一個月后的2009年7月5日,Matrix67的一片博客文章也介紹了這一關卡。我的貼子和 Matrix67 的博文介紹的關卡都是基于2000年國外的一個關于推箱子問題的解答。

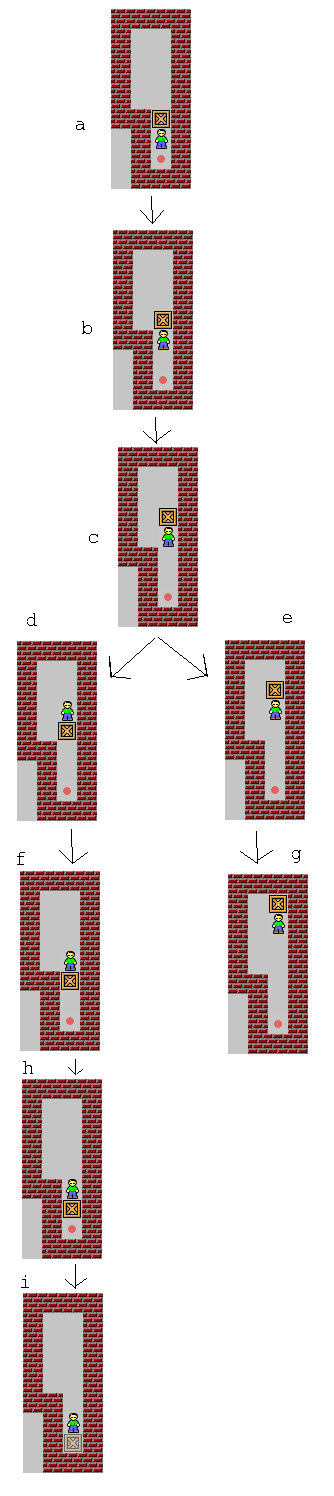
對這個關卡的具體分析這里就不再重復了,簡單的說它就是由一個個的“房間”構成,上圖是三個房間的情況。要過關,最左側一個房間要進入2次,但要進入左一房間1次,就要進入左二房間2次,所以左二房間一共要進入4次。同理,左三房間就要進入8次。一般的,若有n個房間的話,第n個要進入2^n次,于是答案長度便成指數增長了。
這個關卡設計巧妙,讓人感受到推箱子的美。下面我們要介紹一個更美的更簡潔緊湊,但同樣也是具有指數長度的答案的系列關卡。
三
這個更漂亮的系列關卡也是在推箱子玩家里面流傳了很長時間了,有很多變化形式,其中最經典的可能是如下圖所示。

這是???? Aymeric du Peloux 2001年設計的 Picokosmos 第17關。David Holland 在2002年曾分析過這個關卡。Dries De Clercq 在這個基礎上作了名為 Fibo 系列的變形關卡。上圖所示的經典形式不只是一個關卡,而是一系列關卡,關卡可以縱向任意伸長(同時箱子也增加),只要保持箱子總數是偶數個就行了(奇數的時候關卡無解)。若用n表示箱子的數目,隨著n增大,答案步數以n的指數函數增長。
沒有玩過這一關的朋友可以點擊此鏈接在線玩。先提前警告,雖然只有8個箱子,要解出來不太容易。
我是2009年在魔方吧發了前面提到的貼子之后,才注意到這個關卡,當時沒有看到 David Holland 的分析文章,獨立地研究了這一系列關卡的步數。下一節將簡要的介紹一下我的計算方法。
四
上一節提到,這一系列關卡只對偶數個箱子有解。為了便于建立遞推關系,我對箱子位置作了以下微妙調整,使得對奇數也有效。主要有兩處改動:一是最下方一個箱子連同目標移動了一格;二是最上方一側的箱子移下一格(哪一側由奇偶性確定)。如下面所示,分別是4到8個箱子的情形(注意本節的圖和上一節的圖左右反了)。



 本關在線游戲鏈接
本關在線游戲鏈接
 本關在線游戲鏈接
本關在線游戲鏈接
設 n 個箱子的上述關卡的最佳答案需要用 M(n) 步移動,P(n)步推動過關。可以得到下面的遞推關系:
M(n)= M(n-1)+M(n-2)+n +12,????? n 是奇數
M(n)= M(n-1)+M(n-2)+n+10,?????? n 是偶數
P(n)= P(n-1)+P(n-2)+8 .
要得到上面的遞推關系,需要觀察出這系列關卡的過關規律,下面以n=7 為奇數的時候推導以上公式。
首先觀察到這樣一個現象:過關時,箱子把關卡分割成左右兩側不相通的區域。以最佳答案過關時,人是停留在右側區域,如下圖所示的位置。

要想人最后留著左側區域也是可以做到的,但是就是要多用2步移動,推動步數不變,最后位置如下。我們這里述而不證的這一觀察到的結束位置的規律是必須親自解過這一系列關卡才能有體會。如果你還沒來得及解關,下面的遞推關系就會徹底地揭示了求解的秘密了。

下面開始推導遞推關系了。根據實踐規律,當 n=7 個箱子時,前6步必須是 ldDDRU (6步移動,4步推動)。這6步之后,關卡變成下圖。
 ————(1)
————(1)
此時,若忽略最上面兩個箱子,關卡實際上就是 n=5 個箱子的情形。利用 n=5 的時候的解法,可以走到下圖的狀態。
 ————(2)
————(2)
從狀態(1)到狀態(2),基本相當于解一個 n=5 個箱子的關卡,但由于人最后是停在左側區域,根據前面提到的觀察規律,中間需要移動 M(5) + 2 步和推動 P(5) 步。
接下來的步驟必須是 uuuuurrDDLU (移動11步,推動4步)。一般地,則是移動 n+4 步,推動還是4步。經過這11步,得到狀態(3)。
 ————(3)
————(3)
從狀態(3)開始,直到最后過關,相當于解一個 n=6 個箱子的關卡,因為最上方的箱子保持不動。所以余下共移動 M(6) 步,推動 P(6) 步。
經過上面以 n=7 為例的分析,我們得到奇數時的遞推關系:
M(n)=6+M(n-2)+2+n+4+M(n-1)=M(n-1)+M(n-2)+n+12
P(n)=4+P(n-2)+4+P(n-1)=P(n-1)+P(n-2)+8.
偶數的時候原理一樣,具體的推導過程在此就省略了。
有了遞推公式,和 n=4,5 時最佳步數,我們很容易就可以計算出下面的通項公式。
M(n)=(-1)^(n+1)? + (9+sqrt(5)) * a^n + (9-sqrt(5)) * b^n – n -14 ,
P(n)=( (10+4*sqrt(5))/5 ) * a^n +? ( (10-4*sqrt(5))/5 ) * b^n? – 8,
其中 a=(1+sqrt(5))/2 , b=(1-sqrt(5))/2.
下面用 MathJax 顯示一下上述兩個通項公式。
$ M(n)=(-1)^{n+1} + (9+\sqrt{5})\cdot\Big({\frac{1+\sqrt{5}}{2}}\Big)^n + (9-\sqrt{5})\cdot\Big({\frac{1-\sqrt{5}}{2}}\Big)^n-n-14 $ ,
$ P(n)={\frac {10+4\sqrt{5}}{5} } \cdot \Big({\frac{1+\sqrt{5}}{2}}\Big)^n + {\frac {10-4\sqrt{5}}{5} }\cdot\Big({\frac{1-\sqrt{5}}{2}}\Big)^n-8 $ .
從通項公式中,我們可以看出,無論是移動還是推動,答案都是具有指數長度的。
常系數線性遞推關系的求解是比較經典的數學理論了,中學數學競賽常常有這方面的題目,在高等數學里亦有不少應用。這一系列關卡結構緊湊、渾然天成,卻又蘊含如此典型的遞推關系,實在是令人意想不到,堪稱常系數線性遞推關系的求解最有趣的應用之一。
附、第四節7個箱子關卡的最佳答案(306移動,102推動),答案格式說明請參看xsb和lurd格式簡介:
ldDDRUldDDRUdddlUluRurrrddLLUdrruulDlddlUluRuuurrDDLUrdrddLLUlldR
drUrruulDuullDDRUdddlUluRurrrddLLUdrruulDlddlUluRuuuuurrDDLUrdDDL
UrdrddLLUlldRdrUrruulDuullDDRUdddlUluRurrrddLLUlldRdrUrruulDuuuul
lDDRUldDDRUdddlUluRurrrddLLUdrruulDlddlUluRuuurrDDLUdrrddLLUlldRd
rUrruulDuullDDRUdddlUluRurrrddLLUlldRdrUrruulD
GIF動畫演示答案(GIF動畫用YSokoban,irfanview和gifsicle制作,可參看制作推箱子GIF動畫教程):
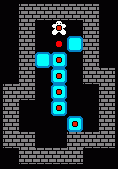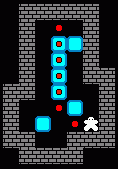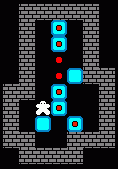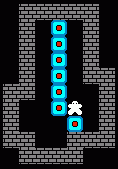
還是這一關,人最后停止在左側區域的答案(308移動,102推動),移動多了2步,最后十來步稍微有區別:
ldDDRUldDDRUdddlUluRurrrddLLUdrruulDlddlUluRuuurrDDLUrdrddLLUlldR
drUrruulDuullDDRUdddlUluRurrrddLLUdrruulDlddlUluRuuuuurrDDLUrdDDL
UrdrddLLUlldRdrUrruulDuullDDRUdddlUluRurrrddLLUlldRdrUrruulDuuuul
lDDRUldDDRUdddlUluRurrrddLLUdrruulDlddlUluRuuurrDDLUdrrddLLUlldRd
rUrruulDuullDDRUdddlUluRurrrddLLUdrruulDlddlUluR