
|
推箱子游戲中半位空間的奇偶屬性與磁鐵效應
作者:鄒永忠2017年6月21日初稿
2019年3月14日整理
通常半個箱位是指占位2×2的小正方形,這里簡稱“半位”。為避免“2個半”的理解歧義,“2個半位”我在這里稱之為“雙半位”或“兩處半位”。 2018年9月12日我在講關卡《二泉映月》的邏輯關系時,已經講過半位空間的一些理論和騰挪要點,今天講的應該算是兩個定理吧,即關于半位空間的奇偶屬性與磁鐵效應,我稱之為半位定理。這兩個半位定理我在十多年前設計半位關卡時發現,前幾年創作《失散之城》系列關卡以及比賽關卡《百尺竿頭》時覺得有必要將其整理成文字。這次在第121期比賽關卡的設計中也運用了這個定理,所以現在把這篇文章整理發出來,相信更多人在看明白這個理論后能解開121期比賽關卡。
一、半位空間具有奇偶不變性。
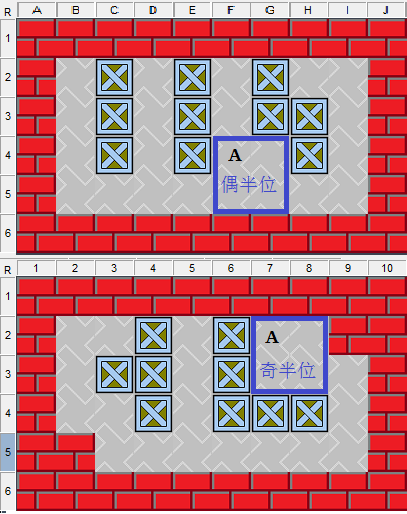
圖1 偶性半位和奇性半位
如圖1,把半位空間左上格A對應的坐標橫軸數字與豎軸數字相加,得到的數是偶數的,我稱之為“偶性半位”或“偶半位”,反之,稱之為“奇性半位”或“奇半位”。半位空間的坐標以左上角即A點的坐標來描述。通常橫向坐標以字母標注,縱向坐標以數字標注,比如圖1的F4半位是偶半位。但這篇文章為便于區分奇偶,部分橫向坐標也以數字標注,F4半位標為6-4半位。
定理1:在一個關卡地圖內,一處半位空間不論移到關卡何處,其奇偶性不變!
證明:有多種方式可以證明這一定理。
1、首先,用圖解的方式直接證明:
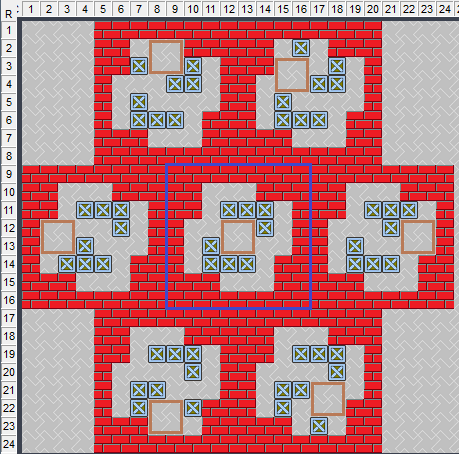
圖2、半位空間移動的幾種常見情形
如圖2,中間的小關卡正中是一個偶性半位空間,通過簡單的變換,可以移動半位空間到6個不同位置。去除對稱重復,我們分析下面圖3的三種情形:
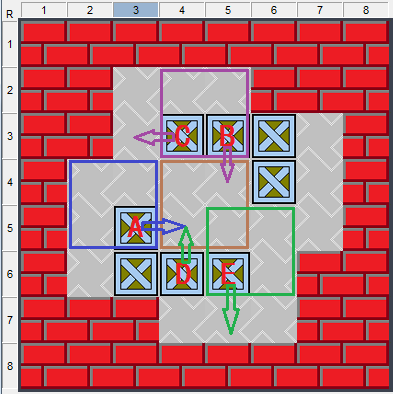
圖3、三種顏色對應三種移位情形
我以前在講半位騰挪理論時已經總結過,當半位空間移動時,其實是木箱向半位空間內移動,將半位空間置換到自己的位置。圖3中,當木箱A向半位空間內移一格,半位空間就向A所在的方向移了2格。一個活的關卡,能夠移動的木箱周圍必然有搬運工可以占據的通道,木箱A之所以可以移動,是因為它左側和右側的通道空置,將木箱A向右推一格,就意味著將右側通道置換到左側,在圖中,就是將第4列通道移到第3列,與原先第2列的通道組成新的半位空間,原先的半位空間從第4列被平移到了第2列,奇偶性不變。
木箱B的移動情形是類似的,但當B向下移動一格時,直觀上并不形成新的半位空間,那是因為木箱C占據了1個角,這個角讓新的半位空間的位置變得不確定。當我們把木箱C向左推1格,其情形就與推動木箱A相同了,半位空間向上平移了2行,其奇偶性不變。如果木箱C向上移1格呢?那正是木箱D和E的情形。
木箱D向上移了1格,使半位空間位置處于待定狀態,如果木箱E再向下移1格,意味著木箱D讓半位空間右移了1格,木箱E讓半位空間下移了一格,半位空間就向右下方向斜移了1格,橫向坐標和縱向坐標各加1,兩者之和,其奇偶性仍然不變。
其實前兩種可以算為一種情形,都是半位空間的平移。第三種是半位空間的斜移。除了這幾種,更多半位空間的移動是比較隱蔽的,比如:
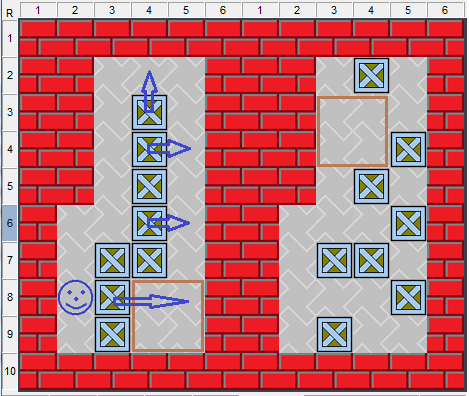
圖4、復雜和隱蔽的半位空間移動
如圖4,半位空間從下方移到上方,似乎看不清中間過程,好像推了這幾只箱子,半位空間突然就跳到上面去了,中間看不到半位空間的連續移動。其實,這種復雜的移動也可以分解成圖3的簡單情形。半位空間在移動過程中其位置處于待定狀態,移動過程中雖然看不到半位空間,但每一步都會產生位置待定的半位空間,且任何待定狀態都是圖3的兩種情形(平移和斜移)之一。每一步狀態分解如下:

圖5、半位空間移動過程分解
移動步驟:
- 第1步:R,半位空間隱藏在待定位置(坐標)2-8和2-6,對應步驟分別為RldR和RluurD;
- 第2步:RR,半位空間隱藏在待定位置2-6和4-8,對應步驟分別為RrlluurD和RrdrU;
- 第3步:RrlluurR,半位空間隱藏在待定位置3-5、2-6和3-7,對應步驟分別為RrlluurRluuRlddrU、RrlluurRluuuurrdddLdlU、RrlluurRllddrrUdlluurD、RrlluurRllddrrUL;
- 第4步:RrlluurRluuR,半位空間隱藏在待定位置3-3、3-5和4-2,對應步驟分別為RrlluurRluuRU、RrlluurRluuRlddrU、RrlluurRluuRluurrdL;
- 第5步:RrlluurRluuRU,半位空間最終移到3-3。
從圖5可以看到半位空間移動的連貫性。半位空間的移動,要么平移,要么斜移,其移動不論怎么隱蔽,都可分解成這兩種狀態,前面已對這兩種狀態的奇偶性進行了闡述。根據上述分析,半位空間的移動,其奇偶性不變。
2、再用反證法進行證明:
假設在一個關卡地圖內,有一處半位空間在移動過程中改變了奇偶屬性,比如從初始狀態的偶半位變為某個狀態的奇半位。由于半位空間的移動是連貫的而不是跳躍的(前面已經證明過,這里不再重復證明),那么不論變化多復雜,用了多少步驟,一定至少有一個步驟是直接從偶半位變成奇半位,我們只截取這個直接產生變化的步驟來觀察:這個偶半位變為奇半位,意味著它向鄰近的方向(橫向或縱向)平移了1格,2×2的半位空間,平移一格產生另一處半位空間,原先空出來的位置加上這新的半位空間,就必然形成2×3的空間(如圖6)。 2×3是一個完整的箱位,這與關卡的半位空間屬性產生了矛盾。當半位騰挪過程中產生1個完整箱位時,必然在關卡內產生死鎖(提前推死目標除外),比如圖6中木箱7-4形成死鎖。綜上所述,這種奇偶改變是不可能的。

圖6、半位空間移動1格
3、我們用兩種方法證明了“定理1”:在一個關卡地圖內,一處半位空間不論移到關卡何處,其奇偶性不變!這個理論有廣泛的應用,在此舉一個例子,如圖7:
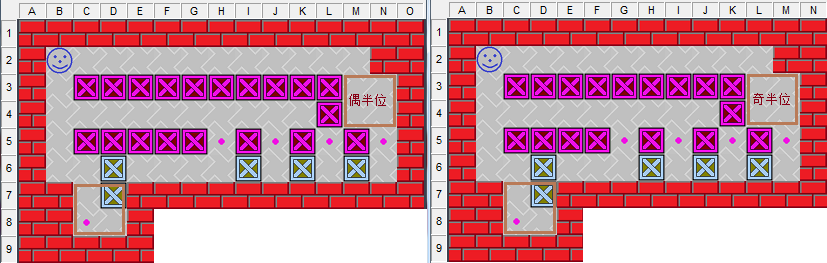
圖7、兩個關卡的死活判斷
如果告訴你這兩關一死一活,怎么快速判斷呢?掌握上述“定理1”后,這兩個關卡孰死孰活就一目了然了。要安全移出D7木箱,就會產生C7半位空間,這個半位是偶半位。左側關卡M3處有一偶半位,移到C7位就有了過關的可能;右側關卡L3處有一奇半位,無法移到C7位,所以它必然是個死關。
二、雙半位空間具有磁鐵效應。
一個關卡地圖內若有雙半位或多半位空間,它們之間具有同性相斥、異性相吸的磁鐵效應。
定理2:在一個關卡地圖內,如果兩處半位可以移動到鄰近位置,具有相同奇偶屬性的雙半位不能合成一個完整箱位,具有不同奇偶屬性的雙半位可以合成一個完整箱位。
證明:這個定理的證明比較容易,我們對同性半位和異性半位分別進行證明。
1、同性半位相斥的證明:
一個關卡地圖內若有兩處以上的半位空間,任意兩處半位移到鄰近位置有兩種情形:(1)錯位相連;(2)對齊相連(橫向對齊與縱向對齊是等價的)。
若是錯位相連,那么如圖8,左側2處半位,右側3處半位,錯位相連的狀態下,在半位空間內任意空格寄存1只木箱,均會阻擋搬運工的通道,形成死鎖。所以同性半位錯位相連不能合成1個完整箱位。
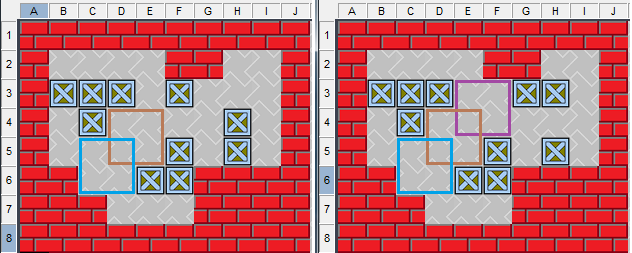
圖8、同性半位錯位相連
若是對齊相連,那么如圖9,D4和F4雙偶半位相連,就形成2×4的空間,這是1.5個箱位,關卡地圖內多出半個箱位,必然在別處產生死鎖(F3木箱死鎖)。
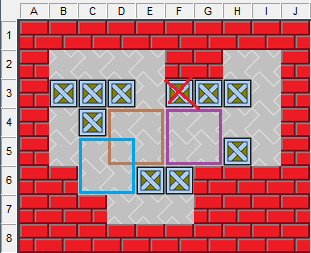
圖9、同性半位對齊相連
綜上所述,同性雙半位相連,要么不能形成有效箱位,要么產生死鎖。同性半位相斥得證。
2、異性半位相吸。
這個是不證自明的,通常意義上的一個完整箱位是2×3的空間,它本身就包含1處偶半位和1處奇半位,也可以說,常規意義的2×3箱位,就是由異性雙半位合成的。如圖10,D3木箱和F3木箱分別向左右各移一格,B2半位(偶半位)和G2半位(奇半位)就在中間連成了1個完整箱位。
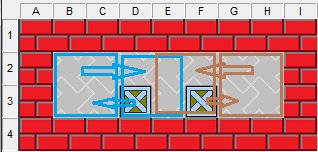
圖10:異性雙半位連成1個箱位
“定理2”是說,具有不同奇偶屬性的雙半位“可以”合成一個完整箱位,并非必然合成一個完整箱位,所以只要找到1個例證,便已證明(其實常規情況下都是可以合成的)。這里需要注意的是:
(1)并非所有完整箱位,都是由異性雙半位合成的。如圖11的綠色方框,這個箱位并非由雙半位合成。
(2)并非所有異性雙半位都能合成1個完整箱位。如圖11紅色方框,這是偶半位空間,由于受到關卡結構的制約,它不能與兩處藍色的奇半位合成完整箱位。
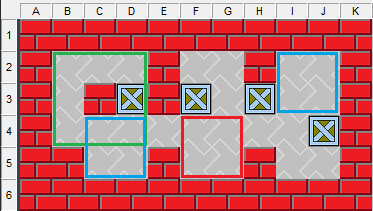
圖11、受限半位
以上分別證明了同性半位相斥、異性半位相吸,定理2得證。
三、舉一些例子具體看看半位定理的應用。
1、關卡《石山之顛》打開后(如圖12右側)在B5和H2有兩處半位空間,B5是奇半位,H2是偶半位。很顯然,兩處半位可以合成一個箱位,合成后的騰挪就輕松一些了。
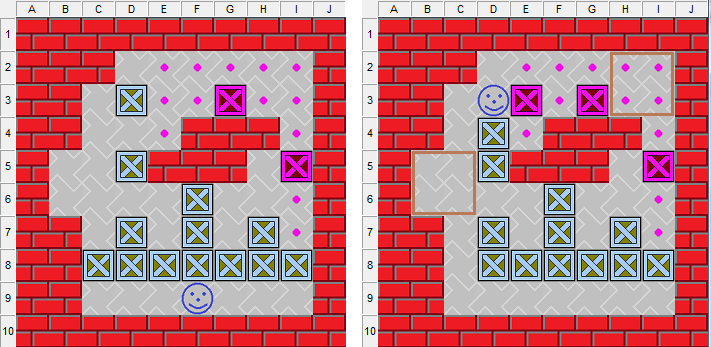
圖12、關卡《石山之顛》
2、《四海飄零》也是雙半位關卡,但它們(B8和F8)都是偶半位,不能合成一個箱位。關卡右上角的結構必需1個完整箱位才能騰挪。理解了半位定理的朋友就會思考:再有一個奇半位就好了。如圖13,我在關卡左下黃框內設置的4個目標點,推到位剛好騰出1處奇半位,這樣就很明顯了,這4個點要先填死。一旦確定這4個點要先填,自然就不會掉入B5木箱推到B3點的陷阱了。
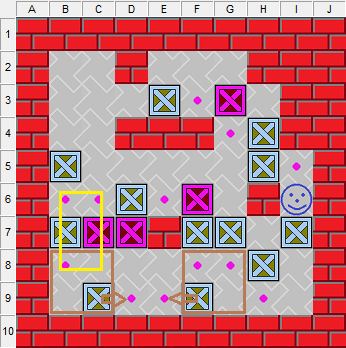
圖13、關卡《四海飄零》
3、第100期比賽關卡《百尺竿頭》有個姊妹關叫《百尺無枝》,它的右側也許會出現3處同性半位空間,如果不了解半位定理,可能會浪費很多時間用來合成箱位。見圖14,《百尺無枝》的右側獨立關《百變右行》,可以很好地詮釋同性半位相斥的定理。
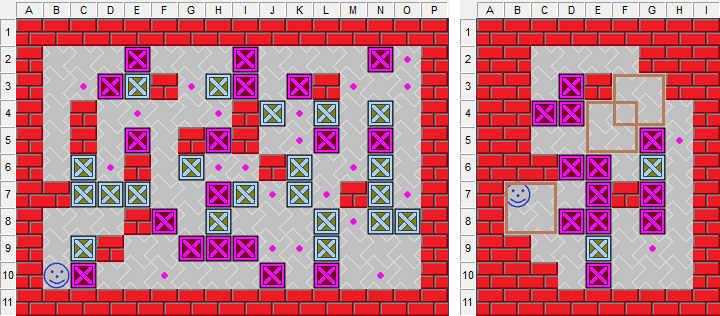
圖14、關卡《百尺無枝》和《百變右行》
由這三個小例子也可看出,半位定理的應用是很廣泛的。運用這一定理來解第121期比賽關卡,更可以達到事半功倍的效果。